Artgineer_기술 배우는 아티스트
[구면기하학] 이각형(진짜 "2"각형)을 만드는 법. 본문
우리는 2각형을 만들 수 있을까?
정답은 "만들 수 있다." 이다.
우선 이각형의 모습부터 보면 이런 모습일 것이다.

이건 타원인데요? 라고 할 수 있는데
타원 맞습니다.
사실 이 타원은

이렇게 Top View 에서 보았을때 타원이었던 것. (투시 없이)
돌려보면 이러한 구체에 그어진 두 직선이라고 할 수 있다.
이게 어떻게 2각형이냐.. 원래 다각형은 직선과 꼭지점으로 이뤄진 도형을 얘기하는데.
라고 할 수 있지만,
그 말은 유클리드 기하학을 기반으로 얘기 했을때 이고, 우리가 오늘 알아볼 것은 구면기하학이다.
구면기하학에서는 두 개의 직선을 그었을때 반드시 두 직선은 만나게 되어있다.
따라서 평행선이라는 개념이 성립하지 않는다.
구면에서는 어떤 직선이든 끝까지 그리다보면 원을 이루는데, 그것을 대원이라고 한다.
그 특징을 이용하여 두 대원은 아무렇게나 그려도 무조건 두 점에서 만나게 되어있으며, 그것이 곧 2각형인 것이다.
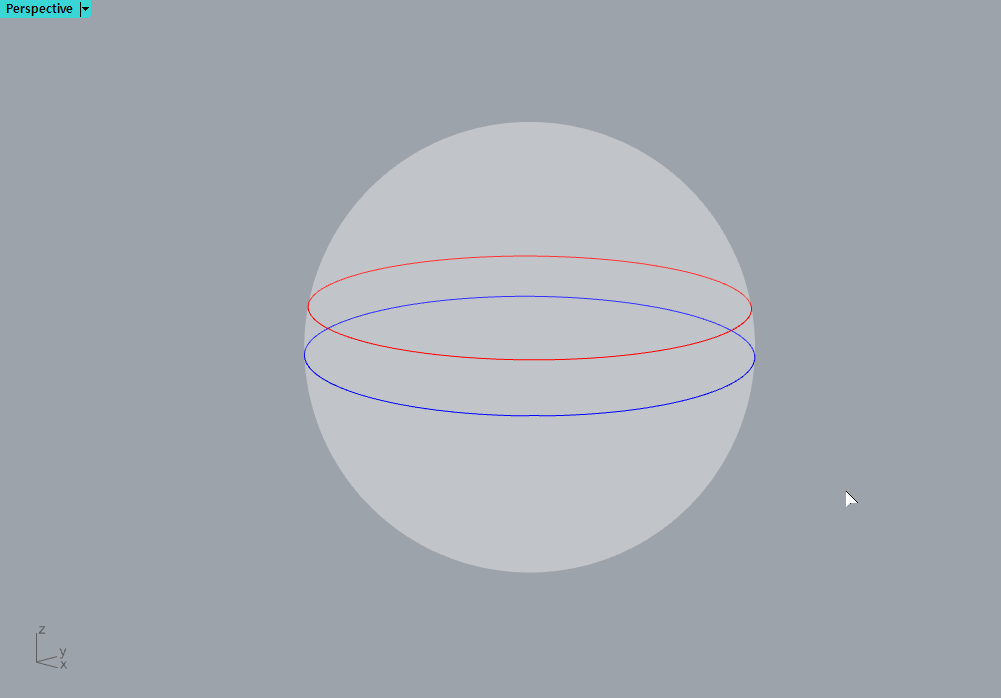
선을 이 예시처럼 그어놓고
이것이야말로 빨간 선과 파란 선이 서로 평행한거 아니냐? 라고 주장할 수 있지만
파란 선은 적도에 위치한 대원. 즉 직선이 맞다고 해도
빨간 선은 사실상 곡선인 것이다.
그 이유를 증명하면 다음과 같다.
좀더 확대해서 빨간 선에 두 점을 찍어보자

두 점을 잇는 가장 최단거리를 그어본다.
최단거리란, 점과 점 사이를 직선으로 이으면 그것이 최단거리일 것이다.
구면에서 최단거리를 긋기 위해서는
구체의 중심을 구해야 한다.

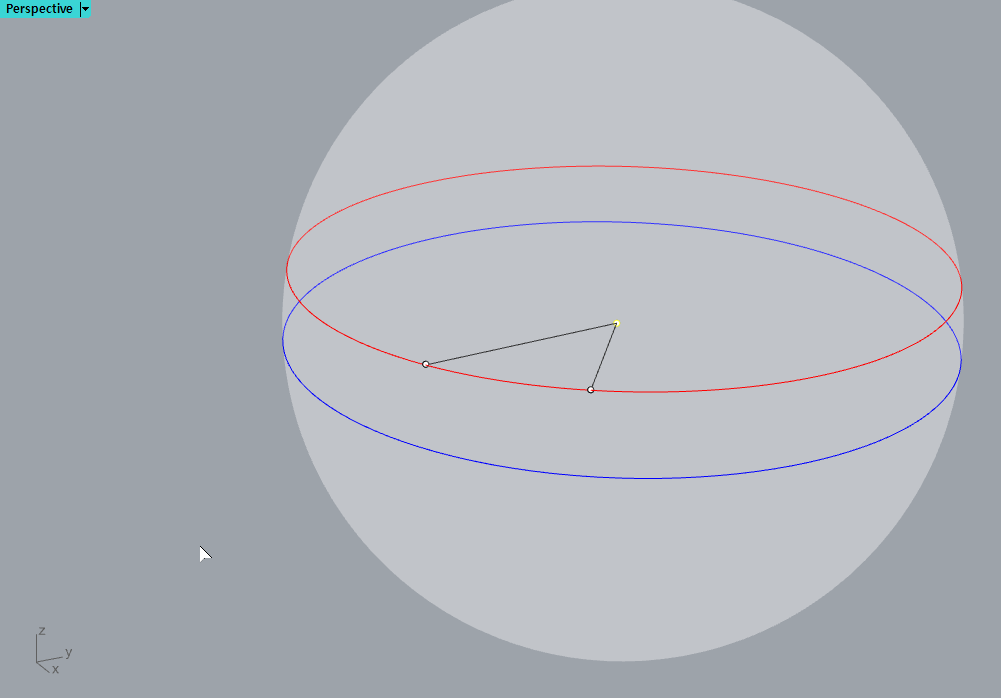
구체의 중심(노란 점)을 찾고, 그 중심점을 기준으로 콤파스를 이용해 두 점을 잇는다고 생각하면 된다.

그럼 이렇게 노란선처럼 두 점 사이에 직선이 그어지는데,
노란선을 확대해서 보면
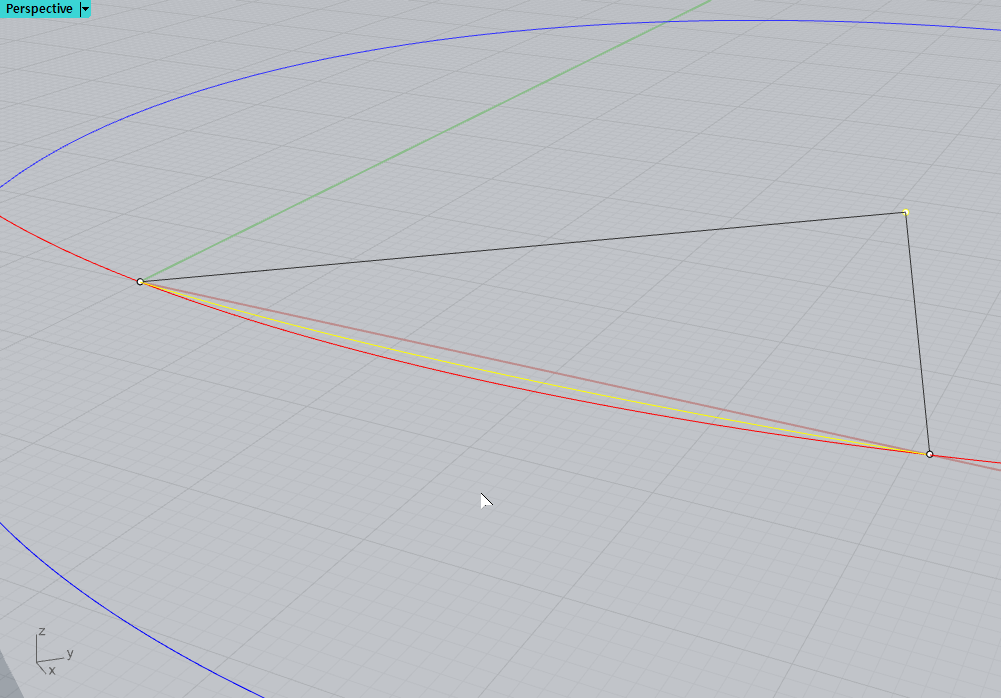
빨간 색 선과 노란 색 측지선 사이의 괴리가 있다.
노란 선(원호)을 완전한 원으로 연장해보면
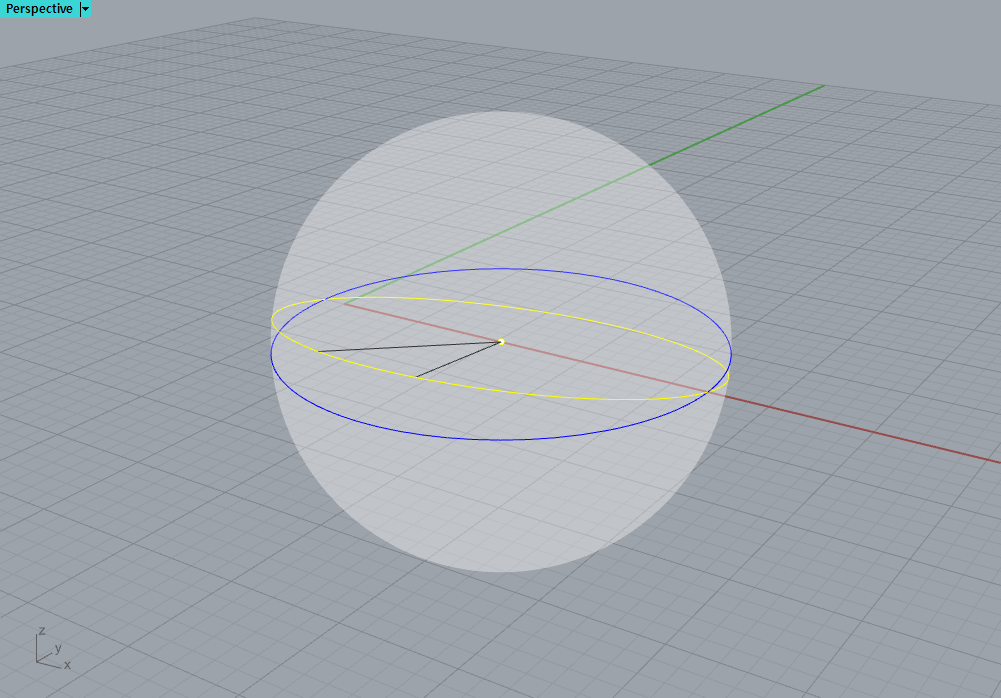
이렇게 노란 대원이 형성되며,
두 개의 대원은 두 점에서 만나게 된다.
이렇게 구면기하학에서는 직선을 그으면 무조건 대원이 되고, 그 대원은 항상 다른 대원과 마주치며 이각형이 그려진다.
오로지 선분으로만 이뤄졌으므로 다각형의 정의에 배반하지 않는다.
이렇게 구면기하학에서는 기존 유클리드기하학에서 볼수 없었던 신기한 현상을 볼 수 있는데,
구면기하학에서는 삼각형의 내각이 180도보다 커질 수 있다.(최소 180도~최대 540도)
구면기하학에서의 삼각형은 다음 시간에 다뤄보도록 하겠다..
'Daily&Life 🌳' 카테고리의 다른 글
| [구조 해석] 구조 검토 독학하기(an unofficial method) (0) | 2025.04.09 |
|---|---|
| 제품 제조업에서 BOM 의 효율성 (0) | 2025.03.18 |
| 무광 차량 “자동세차” 가능? 불가능? 디테일링 제품 추천(내돈내산) (3) | 2024.09.25 |
| 투싼 NX4 페이스리프트 N라인에 블루아머 머드가드 직접 DIY 해보았다. (0) | 2024.09.10 |
| DAG3NEO 허드(HUD) 헤드 업 디스플레이. 신차 계약 시 순정 허드를 놓치고 이 제품을 택한 이유. (0) | 2024.09.09 |





